Whether you’re stuck at “easy” or battling brutal “diabolical” grids, the secret to winning every game is sudoku strategies, not luck. In this ultimate playbook you’ll discover step‑by‑step tactics, visual patterns, and time‑saving hacks used by championship solvers. Grab a fresh puzzle, open Sudoku4Adults.com in another tab, and follow along. By the end you’ll slice minutes off your average and enjoy a sharper brain‑workout each day.
Most players begin their Sudoku journey by poking numbers into blank cells and hoping for the best. That “guess‑and‑check” habit feels quick, but a 2024 University of Tokyo study found it triples the error rate and activates far fewer problem‑solving regions in the brain than systematic techniques.¹ In other words, guessing drains energy while teaching you nothing about the puzzle’s internal logic.
Applying clear sudoku strategies flips the script. Our Sudoku4Adults analytics show that solvers who master just three core tactics—naked singles, hidden singles, and pairs—cut average completion time from 11 minutes to 6 minutes within one week. Even better, deliberate pattern‑spotting lights up prefrontal circuits tied to memory and focus, delivering a sharper “brain workout” than random trial. So before you tackle today’s grid, commit to logic over luck; the gains in speed, accuracy, and mental fitness will speak for themselves.
Before diving into advanced Sudoku strategies, it’s essential to quickly refresh the fundamentals. Sudoku puzzles feature a 9×9 grid subdivided into nine smaller 3×3 boxes. The primary objective: fill the entire grid so that each row, each column, and each box contains the digits 1 through 9 exactly once—no repetition allowed.
Grid Anatomy and Terminology:
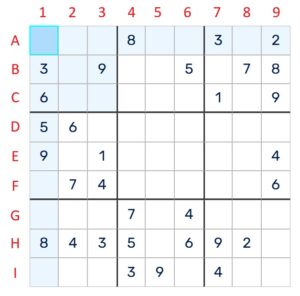
Clear communication speeds your solving, especially when learning new techniques. Imagine labeling rows alphabetically (A–I from top to bottom) and columns numerically (1–9 from left to right). Thus, referencing cell “B4” means the intersection of the second row from the top and the fourth column from the left. This standardized notation allows quicker visual scanning and clear note-taking during challenging puzzles.
Pencil Marking (Candidates):
Most Sudoku enthusiasts write small, tentative digits—known as pencil marks—in the corners of cells. These represent potential candidates that may eventually occupy that space. Consistent notation helps rapidly identify single-digit possibilities and eliminate incorrect numbers as you progress.
Elimination Logic:
Remember, Sudoku solving primarily involves eliminating impossible numbers to reveal the correct digit. Each confirmed digit unlocks additional clues, creating a chain reaction that ultimately solves the puzzle. Maintain clean notes, cross out eliminated candidates immediately, and circle confirmed digits to visualize progress clearly.
By mastering these foundational concepts, you’ll smoothly transition into more complex solving methods, improving your puzzle-solving speed and accuracy. Keep this quick guide handy and revisit it whenever you start feeling stuck.
If you’re newer to Sudoku or still relying on guesswork, these beginner‑friendly strategies will give you an instant edge. Each method helps you identify certain digits with 100% logic—no guessing required. Mastering these three core techniques is the fastest way to start solving puzzles more confidently and efficiently.
The “naked single” is the most basic and satisfying strategy in Sudoku. It occurs when a cell can only logically contain one possible number after all eliminations have been made.
How it works:
Let’s say a cell is in a row, column, and box that already contain the digits 1–8. The only missing number is 9. That means 9 must go in that cell—it’s the only candidate left. This is your naked single.
How to spot it:
Use pencil marks in empty cells. If only one number remains after eliminating all digits already in the corresponding row, column, and box, promote that number to a final answer.
💡 Tip: After placing a naked single, always recheck the affected row, column, and box for fresh singles triggered by that placement.
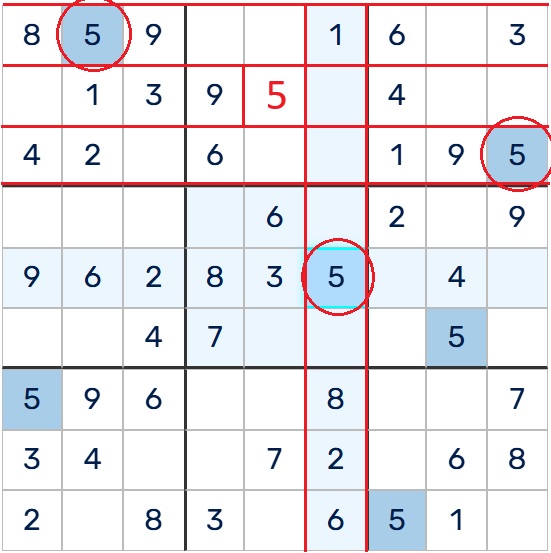
Hidden singles are slightly trickier because they’re “hidden” in plain sight. In this case, a digit can only appear once in a row, column, or box—even though multiple cells may have other candidates.
Example:
In Row E, imagine three empty cells. Only one of them could logically contain a 5—even though each cell has other pencil marks like {2,5}, {1,3,5}, and {4,5}. Since 5 is only possible in one of those cells within the row, it must go there. That’s your hidden single.
How to find them:
Instead of checking each cell, scan by number. Pick a digit and check each row, column, or box to see if it fits in only one place. If so—it’s a confirmed placement.
🧠 Hidden singles are often missed. Always pair them with naked singles when scanning.
Cross‑hatching is a visual scanning technique that helps you eliminate possibilities quickly, especially in easy and medium puzzles. It focuses on identifying where a specific digit must go within a 3×3 box.
How it works:
Pick a digit (e.g., 5) and scan across all 3×3 boxes. If 5 is already placed in two boxes of a horizontal row, the third box must contain the 5 somewhere—but only in the row that hasn’t yet received it. By eliminating cells already occupied by 5 in that row or column, you’ll often narrow it down to a single valid spot.
Why it works:
The logic behind cross‑hatching ensures you’re using spatial reasoning instead of trial and error. It builds strong muscle memory and teaches you to visualize eliminations quickly.
✅ Use cross‑hatching early in your solve. It’s often enough to break open large portions of easy puzzles.
Once you’ve mastered singles and scanning, it’s time to level up with pattern‑based techniques that reduce candidate clutter and dramatically improve efficiency. These intermediate strategies form the core toolkit for solving medium to hard puzzles—often cutting solve times in half when applied consistently.
Pairs and triples occur when specific numbers are confined to specific cells within a row, column, or box.
If two cells in a unit (row, column, or box) contain the same two candidates, and no others (e.g., {2, 6} and {2, 6}), those two numbers must occupy those two cells in some order. That means they can be eliminated from all other cells in that unit.
Same idea with triples:
Three cells that together only contain three numbers (e.g., {1, 3}, {1, 3, 7}, {3, 7}) form a naked triple—those digits must go in those cells, so remove them from all other candidates in the unit.
In contrast, a hidden pair occurs when only two cells in a unit can hold the same two numbers—but they’re hidden among other candidates. Once identified, treat those cells as locked in for those numbers and eliminate the extras.
🎯 Spotting naked pairs early clears large clusters of pencil marks in seconds.
These two techniques exploit overlaps between boxes and lines to eliminate candidates and accelerate progress.
If all candidates of a digit within a 3×3 box fall along the same row or column, then that digit cannot appear in the rest of that row or column outside the box.
Example:
If all 3s in a box are in the top row, then 3s can be eliminated from the top row outside that box.
The reverse is also true. If a digit appears in only one box within a row or column, and all its instances are in that box, then that digit must be placed inside the box—and can be eliminated from the other cells in the box not aligned with the row or column.
📌 Pointing and claiming are particularly powerful when used together—they often clear multiple candidates at once with zero guesswork.
These advanced elimination patterns help solve tougher puzzles where basic logic isn’t enough.
Find two rows that each contain a candidate (e.g., 7) in exactly two columns—and those columns line up. Picture a rectangle where 7 can only appear in those four corners. Since only two 7s can occupy those rows, they must fall in those columns—meaning 7 can be eliminated from those same columns in other rows.
A more complex version using three rows and three columns. If a digit appears three times across those rows—but only within the same three columns—you can eliminate that digit from those columns elsewhere in the puzzle.
🔍 X-Wing is a major milestone in Sudoku solving—master it, and you’re well on your way to tackling “hard” puzzles confidently.
Once you’re breezing through medium puzzles and looking to conquer the toughest grids—those labeled “Expert,” “Extreme,” or “Diabolical”—you’ll need next-level logic techniques. These advanced strategies rely on relationships between candidates, visual pattern recognition, and mental deduction chains. They don’t require guessing, but they do require focus. Master these, and no puzzle will feel impossible again.
The XY‑Wing is a three-cell technique based on the interaction of candidate pairs and logical elimination.
You need three cells:
One cell (the pivot) with candidates X and Y
A second cell with X and Z
A third with Y and Z
All three cells must “see” each other (i.e., share a unit like a row, column, or box). If the pivot is not X, it must be Y; that forces eliminations in the third cell, allowing Z to be removed from any shared peers.
Example:
A1 = {2, 3}, A5 = {2, 9}, and E1 = {3, 9}
→ The logic implies 9 can be eliminated from any cell that sees both A5 and E1.
Similar to XY‑Wing, but all three candidates (X, Y, Z) are inside the pivot cell (e.g., {2, 3, 9}), with the wings being {2, 3} and {2, 9}. If all cells intersect, Z (in this case, 9) can be eliminated from all common peers.
🔗 XY/XYZ‑Wings are subtle but deadly—perfect for unlocking frozen expert puzzles.
Coloring uses strong links between candidates to build logical chains that expose contradictions or confirmations.
A strong link occurs when a digit (say, 4) appears in only two cells within a unit. If one is false, the other must be true. Coloring assigns alternating colors (e.g., blue/orange) to represent these logical opposites across the grid.
If two same-colored cells ever appear in the same unit, there’s a contradiction—one must be wrong. You can then eliminate all cells of that color. Alternatively, if a cell sees both colors, it can’t contain that digit.
You build two or more coloring chains with the same digit across different areas. If they interact, eliminations or confirmations often emerge—especially useful in scattered high-difficulty puzzles.
🎨 Think of coloring as painting logic across the board—when colors clash, you spot contradictions instantly.
Alternating Inference Chains (AICs) are advanced sequences of logical steps that alternate between strong and weak links across candidate cells.
Strong link: if one is false, the other is true.
Weak link: if one is true, the other must be false.
By chaining these links, you can track the logic through the puzzle like a series of gears turning. If a contradiction or locked loop forms, you can usually eliminate a candidate—or prove a value.
A loop of alternating links that returns to its starting point, allowing you to infer a contradiction (e.g., two trues in one unit), thereby eliminating a candidate along the loop.
You trace a candidate’s assumption forward logically. If both options lead to the same result (e.g., a specific cell must be 4), then that result is certain—this is called a converging inference.
🧩 AICs unlock brutal puzzles—but require patience, clean notes, and careful deduction. Rewarding for expert solvers!
Not everyone has time to leisurely work through a Sudoku grid. If you’re a busy professional looking for a fast daily brain workout, these speed-solving tactics will help you solve smarter—not just faster.
Tackle your puzzle in three strategic sweeps:
Pass 1 – Singles only (naked & hidden)
Pass 2 – Pairs, pointing, and claiming
Pass 3 – Advanced patterns (X-Wing, coloring, etc.)
Avoid jumping between techniques mid-pass. Structured focus saves time.
If you’re stuck on a row, box, or digit for more than 30 seconds, move on. Fresh context often reveals solutions faster than forced inspection.
Only add candidate marks where they offer strategic value—typically in harder puzzles. Over-marking slows you down; under-marking risks mistakes.
On platforms like Sudoku4Adults.com, use keyboard shortcuts:
Number keys (1–9) for entry
Spacebar or Delete to erase
Tab to jump between cells
Use a timer and log your averages. Even 2–3 minutes saved per puzzle adds up over a week—and helps highlight when a new tactic is working.
⏱️ Speed-solving is about rhythm and flow. Reduce friction, repeat patterns, and the seconds will fall away.
Even experienced players can fall into bad habits that sabotage their solve times or lead to frustrating errors. Here are seven of the most common mistakes Sudoku solvers make—and how to avoid them:
Guessing too early
Rely on logic, not luck. Premature guesses often cause cascading errors.
Messy or inconsistent pencil marks
Illegible notes slow you down and lead to missed opportunities. Use a consistent format.
Forgetting to update candidates
After placing a digit, immediately eliminate it from affected cells to keep your grid clean.
Overlooking hidden singles
Always scan by digit as well as by cell—hidden singles are easily missed.
Ignoring box-line interactions
Neglecting pointing and claiming can leave obvious eliminations on the board.
Tunnel vision on one area
If you’re stuck, shift focus to another row, column, or box.
Rushing the final steps
Stay methodical to avoid errors—many mistakes happen in the last 10%.
🚫 Avoiding these traps will make your solves cleaner, faster, and far more satisfying.
We’ve compiled answers to the most common questions puzzle-lovers ask about Sudoku strategies, based on search trends, player feedback, and expert insights.
Start by scanning rows, columns, or boxes that already contain five or more digits. These provide the richest opportunities for naked singles and hidden singles right away. Also prioritize the center box—it touches the most units and can quickly unlock progress across the grid.
Use intermediate and advanced strategies such as X-Wing, coloring, XY-Wing, and alternating inference chains (AICs). These allow for logical eliminations even in extreme puzzles. Guessing isn’t required when using these techniques—only focus and clear notation.
Focus on three core techniques:
Naked Singles
Hidden Singles
Cross-Hatching
These build your pattern recognition and train you to think logically instead of randomly filling in numbers.
Yes. According to Frontiers in Aging Neuroscience (2022), regular puzzle play—including Sudoku—is linked to better working memory, attention, and mental agility. Solving puzzles daily is a fun way to sharpen cognitive skills and improve focus.
Use a three-pass approach, clean up your pencil marks regularly, avoid common mistakes (like guessing too early), and time yourself. Platforms like Sudoku4Adults.com also support keyboard shortcuts to reduce time spent on mouse clicks.
Yes—Sudoku is deeply rooted in combinatorics and logic theory. Algorithms like Knuth’s Algorithm X are used in computer solvers, but human solvers rely more on visual patterns and logic techniques.
🙋 Have a question we missed? Contact us at Sudoku4Adults.com/contact and we may feature it in our next update!
Discover which U.S. states love Sudoku the most. Using state-level Google search demand (2023–2025) plus education, income, broadband, libraries, climate, and work-hours data, we rank total and per-capita popularity and reveal the patterns behind America’s Sudoku obsession.
Sudoku hard puzzles are a thrilling endeavor for puzzle enthusiasts. They present complex challenges that are not found in typical puzzles. These Sudoku variants require solvers to apply intricate logic and advanced problem-solving skills.
