How to Make a Sudoku Puzzle Manually (Step-by-Step + Expert Tips)
Creating your own Sudoku puzzle might sound intimidating, but it's easier than you think. In this comprehensive guide, you'll learn exactly how Sudoku puzzles are generated, how to make your own from scratch, and how to ensure it has only one solution. Whether you're crafting a puzzle for fun or publication, this guide has you covered.
How to Make a Sudoku Puzzle Manually
Ever stared at a Sudoku puzzle and thought, “Who even creates these?” Here’s the truth: you can. With a little logic, patience, and guidance, you can design your own Sudoku puzzle from scratch — and it might just be more satisfying than solving one.
In this expert guide, you’ll learn exactly how to create a Sudoku puzzle manually, understand how Sudoku puzzles are generated, and master the process step-by-step. No fancy tools. No coding. Just logic, a pencil, and this guide.
Understanding What Makes a Sudoku Puzzle
Before you start crafting, let’s understand what defines a Sudoku puzzle:
It consists of a 9×9 grid, divided into nine 3×3 subgrids (boxes).
The goal is to fill the grid so each row, column, and box contains the digits 1 through 9 exactly once.
A proper puzzle must have only one valid solution.
This might sound easy to replicate, but creating a puzzle that is both challenging and solvable without guessing requires careful design.
Tools You Need to Create Sudoku by Hand
To begin crafting a Sudoku puzzle manually, gather the following:
A blank Sudoku grid (printable sheets or graph paper)
Pencil & eraser (you’ll need to make changes)
Patience and logic!
(Optional) Colored pens or highlighters
(Optional) A Sudoku solving tool (for validation only, not generation)
Step 1: Fill a Blank Grid With a Complete Solution
This is the most critical part of making a Sudoku puzzle. If the grid isn’t fully filled with a valid solution, everything else will fall apart.
A. Use Logic, Not Randomness
Random placement of digits is tempting, but it almost always results in a broken puzzle. You’ll end up violating the core rule that each digit must appear only once per row, column, and 3×3 box. Instead, approach it logically and methodically.
You can think of this process as solving a puzzle in reverse: instead of deducing values from limited information, you’re constructing a grid where all values are already known but must obey strict constraints.
Start with a plan to place each number from 1 to 9 multiple times across the board. Try focusing on filling just one number at a time across the grid in various boxes, while ensuring they don’t clash.
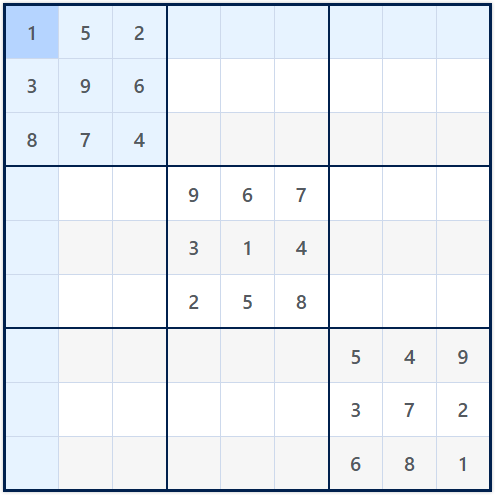
B. Start With Diagonal Boxes
A proven method to simplify this process is to begin by filling the three diagonal 3×3 boxes:
Top-left (cells [0,0] to [2,2])
Center (cells [3,3] to [5,5])
Bottom-right (cells [6,6] to [8,8])
These boxes do not share rows or columns, making it easier to populate each with the digits 1 through 9 without concern for overlap.
Use a shuffled list of the digits 1-9 for each diagonal box. Write them in without repeats, and double-check that you have each digit exactly once in the 3×3 square.
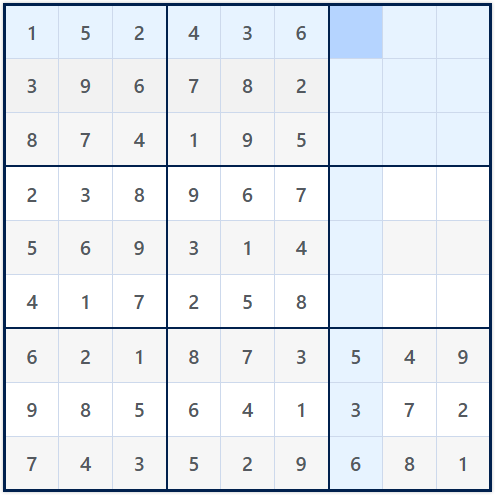
C. Fill the Remaining Grid
Now it gets interesting.
Begin filling out the remaining boxes, one at a time. Use the following techniques:
Row scanning: Check what numbers already exist in the row.
Column scanning: Check for duplicates in the column.
Box scanning: Make sure the number isn’t repeated in the 3×3 box.
Pencil marking: List possible candidates in each empty cell, then narrow them down by eliminating options using logic.
Try to move in layers: fill all 3×3 boxes along the top row of boxes, then the middle, then the bottom. It helps to treat the grid like a Sudoku solver would: fill in what you know, then update possibilities.
Troubleshooting: If you hit a dead end, go back a few steps and re-check your placements. It’s common to make small placement mistakes early that snowball into unsolvable situations.
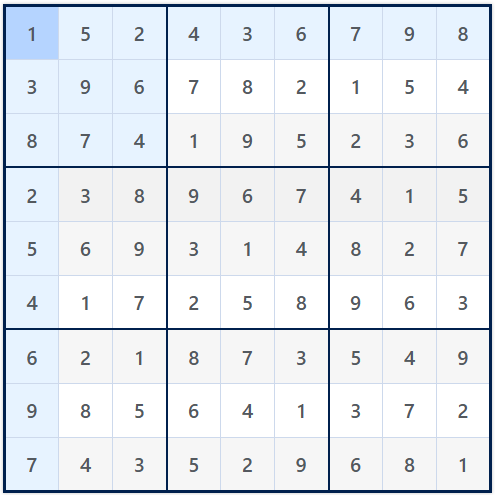
D. Check for Rule Compliance
Once the grid is fully filled:
Go through each row: confirm that digits 1-9 appear without repetition.
Do the same for each column.
Finally, verify each 3×3 box.
If everything checks out, congratulations! You now have a valid Sudoku solution grid, the foundation for your custom puzzle.
Step 2: Remove Numbers Strategically
This is where your solution becomes a real Sudoku puzzle. The idea is to strategically remove numbers while preserving a unique solution.
A. Remove Symmetrically (Optional but Recommended)
While not required, symmetry is a hallmark of professional puzzles. It adds a visual balance and is common in newspaper and magazine Sudoku.
To do this, whenever you remove a cell, remove its mirror position across the central point. For example:
Remove cell [0,1] and also remove [8,7].
Remove cell [3,3] and also [5,5].
This process maintains visual aesthetics and helps with balance.
B. Do It Slowly and Test Often
Start by removing one pair of numbers at a time. After every 4 to 5 removals:
If removing a particular clue leads to multiple possible solutions, you should restore it and choose a different one.
Methodical removal is better than removing 30 numbers at once and trying to salvage it later. Think of it like sculpting: you’re trimming the excess to reveal the challenge hidden within.
C. Keep Track of Difficulty
The number of clues left in the puzzle generally defines its difficulty:
But difficulty is also defined by the type of logic required. A puzzle with only 30 clues can still be easy if solving it requires basic techniques.
You can tailor the challenge by selectively removing numbers that require:
Advanced solving methods (e.g., X-Wing, Swordfish)
Longer logical chains
Minimal starting points, forcing solvers to look deeper
Remember: the goal isn’t just to make it hard, but to make it fun and rewarding.
Step 3: Test for Uniqueness and Difficulty
Your puzzle looks ready, but you’re not done yet. Testing is the final and arguably most important step.
A. Solve the Puzzle Yourself
Put your grid to the test using only logic:
Naked singles: Only one possible number fits in a cell.
Hidden pairs: Two numbers appear only in the same two cells of a row/column/box.
Pointing pairs/triples: Candidate elimination across box/line interactions.
Box-line reduction: Eliminate options from other boxes based on shared rows/columns.
If you ever need to guess, it’s a red flag that your puzzle may not be logically solvable or has multiple solutions.
B. Ask Someone Else to Solve It
Let a friend, family member, or online community solve your puzzle. Observing their strategy can help you:
C. Validate With a Solver Tool
For final confirmation, use a Sudoku validator online. These tools confirm whether your puzzle:
Use our free, easy to use sudoku validator tool to ensure your puzzle is correct and unique.
After testing, your puzzle is officially ready to publish, print, or challenge your friends!
Related Posts